设函数f(x)连续,给出下列四个条件:
①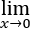 (|f(x)|-f(0))/x存在; ②
(|f(x)|-f(0))/x存在; ②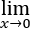 (f(x)-|f(0)|)/x存在;
(f(x)-|f(0)|)/x存在;
③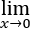 |f(x)|/x存在; ④
|f(x)|/x存在; ④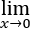 (|f(x)|-|f(0)|)/x存在;
(|f(x)|-|f(0)|)/x存在;
其中能得到“f(x)在x=0处可导”的条件个数是【 】
A、1
B、2
C、3
D、4
设函数f(x)连续,给出下列四个条件:
①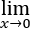 (|f(x)|-f(0))/x存在; ②
(|f(x)|-f(0))/x存在; ②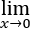 (f(x)-|f(0)|)/x存在;
(f(x)-|f(0)|)/x存在;
③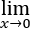 |f(x)|/x存在; ④
|f(x)|/x存在; ④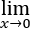 (|f(x)|-|f(0)|)/x存在;
(|f(x)|-|f(0)|)/x存在;
其中能得到“f(x)在x=0处可导”的条件个数是【 】
A、1
B、2
C、3
D、4
D
【解析】
解答过程见word版
设单位质点P,Q分别位于点(0,0)和(0,1)处,P从(0,0)处出发沿x轴正向移动,记G为引力常量,则当质点P移动到点(l,0)时,克服质点Q的引力所做的功为【 】
设函数f(x,y)连续,则∫-2²dx ∫4-x²4f(x,y)dy=【 】
设函数f(x),g(x)在x=0的某去心领域内有定义且恒不为零.若x→0时,f(x)是g(x)的高阶无穷小,则当x→0时【 】
如果对微分方程y''-2ay'+(a+2)y=0的任一解y(x),反常积分∫0+∞y(x)dx均收敛,则a的取值范围是【 】
已知函数f(x)=∫0xet² sintdt,g(x)=∫0xet²dt∙sin²x,则【 】
设函数z=z(x,y)由z+lnz-∫yxe-t² dt=0确定,则∂z/∂x+∂z/∂y=【 】
设矩阵A=,已知1是A的特征多项式的重根.(1)求a的值;(2)求所有满足Aα=α+β,A²α=α+2β的非零列向量α,β.
设Σ是由直线 绕直线 (t为参数)旋转一周得到的曲面,Σ1是Σ介于平面x+y+z=0与x+y+z=1之间部分的外侧,计算曲面积分∬Σ1xdydz+(y+1)dzdx+(z+2)dxdy.
设函数f(x)在区间(-1,1)内有定义,且f(x)=0,则【 】
设函数f(x)在区间(-1,1)上有定义,且f(x)=0,则【 】
证明:(f(x0+h)-f(x0-k))/(k+h)存在的充要条件为f在x0处可导.
设函数f(x)在x=0处连续,且(xf(x)-e2sinx+1)/(ln(1+x)+ln(1-x))=-3证明:f(x)在x=0处可导,并求f'(0).
已知f'(3)=2,则(f(3-h)-f(3))/2h=________.
设f(x)在x=a处可导,则(f(a+x)-f(a-x))/x等于【 】
设f(x)可导,F(x)=f(x)(1+|sinx|),欲使F(x)在x=0可导,则必有【 】
设当x=0时,f(sinx)= f2(sinx),f'(x)≠0,则f(0)=__________.